Introduction to machine learning
Overview
Teaching: min
Exercises: minQuestions
Objectives
What is machine learning?
Machine learning comprises a variety of tools and methodologies designed to uncover patterns within datasets. This lesson aims to introduce a selection of these techniques, although there exist numerous others beyond the scope of this session. These techniques can be broadly categorised into two main groups: predictors and classifiers. Predictors are employed to forecast a value or a set of values based on a given set of inputs. For instance, they may predict the cost of an item considering economic conditions and the price of raw materials, or forecast a country’s GDP based on its life expectancy. On the other hand, classifiers are tasked with categorised data into distinct groups. For example, they might discern visible characters within an image of written text, or determine whether a message is spam or legitimate.
Training Data
Many machine learning systems, although not all, acquire knowledge by processing a sequence of input and output data, which they then utilize to construct a model. The mathematical underpinnings of machine learning are agnostic to the nature of the data, as long as it can be represented numerically or categorised. Examples of such applications include:
- Estimating an individual’s weight based on their height
- Predicting commute durations given prevailing traffic conditions
- Forecasting housing prices based on stock market fluctuations
- Distinguishing between spam and legitimate emails
- Identifying whether an image contains a person or not
Typically, these models require extensive training with hundreds, thousands, or even millions of examples before they achieve sufficient accuracy for practical predictions or classifications. Some systems undertake training as a one-time process, resulting in the creation of a model. Others may continuously refine their training through real-world system usage and human feedback also know as reinforcement learning. For instance, every time a user labels an email as spam or not spam, they likely contribute to further training of the spam filter’s model.
Types of output
Predictors will usually involve a continuous scale of outputs, such as the price of something. Classifiers will tell you which class (or classes) are present in the data. For example a system to recognise hand writing from an input image will need to classify the output into one of a set of potential characters.
Machine learning vs Artificial Intelligence
Artificial Intelligence encompasses systems with generalized intelligence, theoretically capable of solving a wide array of problems. However, AI is a broad term with varying interpretations. Machine learning systems, on the other hand, are typically trained to address specific problems. While they may exhibit learning behaviour, they lack the generalized intelligence to solve any problem a human could tackle. These systems often require hundreds or thousands of examples to learn and are limited to relatively straightforward classifications. In contrast, a human-like system could learn from a single example. Another definition of Artificial Intelligence traces back to the 1950s and Alan Turing’s “Imitation Game.” According to this concept, a system could be deemed intelligent if it could deceive a human into believing they were interacting with another human when in fact, they were conversing with a computer. Modern endeavours in this realm are approaching the point of successfully fooling humans, yet achieving a machine with full human-like intelligence remains a distant prospect.
Applications of machine learning
Machine learning in our daily lives
- Image Recognition
- Object Detection
- Character Recognition
- Insurance Premiums
- Energy usage
Example of machine learning in research
- Detecting water leaks in pipes.
- Cancer detection.
- Improving farming productivity.
Limitations of Machine Learning
Garbage In = Garbage Out
In Computer Science, there’s a well-known saying: “Garbage In = Garbage Out.” This adage highlights the principle that if the input data provided is of poor quality or irrelevant, the resulting output will likely be similarly flawed. For example, if we attempt to train a machine learning system to establish a correlation between two variables that are fundamentally unrelated, the model may still generate a semblance of a connection, but the output will lack meaningful significance. This is often apparent when the model’s output appears erratic or seemingly random.
Bias or lacking training data
The input data may also lack sufficient diversity to encompass all potential scenarios. Biases present in the data collection process can subsequently manifest in the machine learning system. For instance, if data on crime reporting is gathered, it may skew towards wealthier areas where incidents are more likely to be reported. Historical data might be inadequate in terms of coverage or relevance to the specific context being analysed. For example, imagine creating a model to transcribe written text from historical documents. If the model is trained solely on documents from the 1950s to 2000, it may perform well when tested on similar samples from that era. However, testing the model on pre-1950s material might yield poor results because handwriting styles and language usage evolve over time.
Extrapolation
We can only confidently forecast outcomes for data that falls within the range of our training data. When attempting to extrapolate beyond the scope of our training data, it’s likely that our predictions will be inaccurate. An easy way to see this is to plot your training data based on it features along with the sample you want to analyse. If the sample is no where near your data then you could consider this sample an outlier.
Over fitting
Sometimes ML algorithms become over trained to their training data and struggle to work when presented with real data. Meaning that the model has focused too much on certain characteristics that determine said task, but these may not be applicable when it is used to predict on the test set. This again results in some random predictions. Therefore, its critical not to over train (train for too long) your model.
Inability to explain answers
Many machine learning techniques will give us an answer given some input data even if that answer is wrong. Most are unable to explain any kind of logic in arriving at that answer. This can make diagnosing and even detecting problems with them difficult.
Key Points
Clustering
Overview
Teaching: min
Exercises: minQuestions
Objectives
Clustering
Clustering involves the categorisation of data points based on their similarities, offering a robust method for detecting patterns within datasets. It typically operates without the need for training, distinguishing it as an unsupervised learning approach. This lack of training requirement facilitates swift application..
Applications of Clustering
- Looking for trends in data
- Data compression, all data clustering around a point can be reduced to just that point. For example, reducing colour depth of an image.
- Pattern recognition
K-means Clustering
he K-means clustering algorithm is a straightforward technique aimed at pinpointing the centroid of each cluster. It achieves this by seeking a point that minimizes the distance between the centroid and all the points within the cluster. While the algorithm requires a predetermined number of clusters to identify, a common approach involves experimenting with various cluster numbers and employing additional tests to determine the optimal configuration.
Lets look at our data
So firstly lets have a look at the features within our dataset:
> data("iris") ## load in data
> head(iris) ## show just the first few rows
Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa
we could also compare different features, lets compare Petal length against Petal width:
> plot(iris$Petal.Length, iris$Petal.Width, pch=21, bg=c("red","green3","blue")[unclass(iris$Species)], main="Iris Data") ## plot two features against each other
> legend("top", levels(iris$Species), pch = 21,col = c("red","green3","blue")) ### well of course we want a legend
As observed, the “setosa” species appears to cluster more distinctly, while there is some overlap or noise between “versicolor” and “virginica,” despite their apparent similarity. Now, let’s execute the model. Since the kmeans function is included in the base package of R, there’s no need to install any additional packages. When using the kmeans function, it’s essential to specify the “centers” parameter, which represents the number of clusters we intend to create. In this scenario, we know that the appropriate value is 3. Let’s proceed by setting it accordingly. Now lets try and cluster all the features
> set.seed(0)
> irisCluster <- kmeans(iris[,1:4], center=3, nstart=20) ### take only the data columns that we want
> irisCluster
Now lets have a look at the 3 clusters the model has come up with. To do this we use a library called “cluster”, so we can see the regions/groups that the points have been separated into.
> library(cluster)
> clusplot(iris, irisCluster$cluster, color=T, shade=T, labels=0, lines=0) ## special kind of plot for showing clusters
Limitations of K-Means
- Requires number of clusters to be known in advance
- Struggles when clusters have irregular shapes
- Will always produce an answer finding the required number of clusters even if the data isn’t clustered (or clustered in that many clusters).
- Requires linear cluster boundaries
Advantages of K-Means
- Simple algorithm, fast to compute. A good choice as the first thing to try when attempting to cluster data.
- Suitable for large datasets due to its low memory and computing requirements.
Spectral Clustering
Spectral clustering is a method utilised in machine learning and data analysis to cluster data points according to their likeness. This approach entails converting the data into a format where clusters are discernible, followed by applying a clustering algorithm to this altered data. In the R Programming Language, spectral clustering achieves this transformation by leveraging the eigenvalues and eigenvectors of a similarity matrix.
Spectral clustering works by transforming the data into a lower-dimensional space where clustering is performed more effectively. The key steps involved in spectral clustering are as follows:
Affinity Matrix
Begin with a dataset containing data points. Calculate an affinity or similarity matrix that measures the connections between these data points, indicating their level of similarity or correlation. This matrix encapsulates the degree of similarity or relationship between each pair of data points. Popular methods for computing affinity include Gaussian similarity, k-nearest neighbors, or a custom similarity function provided by the user.
Graph Representation
View the affinity matrix as the adjacency matrix of a weighted undirected graph. In this graph, each data point represents a vertex, and the edge weight between vertices indicates the similarity between the respective data points.
Laplacian Matrix
Construct the graph Laplacian matrix, which captures the connectivity of the data points in the graph. There are two main types of Laplacian matrices used in spectral clustering.
Unnormalized Laplacian: L = D – A, where D is the degree matrix and A is the affinity matrix. The degree of a vertex is the sum of the weights of its adjacent edges. Normalized Laplacian: L_norm = I – D^(-1/2) * A * D^(-1/2), where D^(-1/2) is the diagonal matrix of the inverse square root of the node degrees.
Eigenvalue Decomposition
Compute the eigenvalues (λ_1, λ_2, …, λ_n) and the corresponding eigenvectors (v_1, v_2, …, v_n) of the Laplacian matrix. You typically compute a few eigenvectors, corresponding to the smallest non-zero eigenvalues.
###Embedding
Use the selected eigenvectors to embed the data into a lower-dimensional space. The eigenvectors represent new features that capture the underlying structure of the data. The matrix containing these eigenvectors is referred to as the spectral embedding.
### Using Euclidean distance as a similarity measure
> similarity_matrix <- exp(-dist(iris[, 1:4])^2 / (2 * 1^2))
### Compute Eigenvalues and Eigenvectors
> eigen_result <- eigen(similarity_matrix)
> eigenvalues <- eigen_result$values
> eigenvectors <- eigen_result$vectors
### Choose the First k Eigenvectors
> k <- 3
> selected_eigenvectors <- eigenvectors[, 1:k]
### Apply K-Means Clustering
> cluster_assignments <- kmeans(selected_eigenvectors, centers = k)$cluster
### Add species information to the clustering results
> iris$Cluster <- factor(cluster_assignments)
> iris$Species <- as.character(iris$Species)
### Plot the
> library(ggplot2)
> ggplot(iris, aes(Sepal.Length, Sepal.Width, color = Cluster, label = Species)) + geom_point() +
geom_text(check_overlap = TRUE, vjust = 1.5) +
labs(title = "Spectral Clustering with k-means of Iris Dataset",
x = "Sepal Length", y = "Sepal Width")
Exercise: Increasing the number of cluster centres
Have ago at increasing the number of centres for you K-means cluster to find. What does it look like if you try 4,5 or even 6? How could we find the most optimal amount?
Key Points
Dimensional Reduction
Overview
Teaching: min
Exercises: minQuestions
Objectives
Dimensionality Reduction
Dimensionality reduction serves as a potent technique for analysing and visualising data sets, especially when dealing with high-dimensional data such as datasets or outputs from machine learning models. These methods effectively reduce the number of features in your data, which is crucial considering that visualising anything beyond two dimensions is challenging. For this section we will focus on two commonly used methods for dimensionally reducing your data, One being Principal Component analysis (PCA) a linear method and second t-SNE a non-parametric/ non-linear method.
Examine the dataset
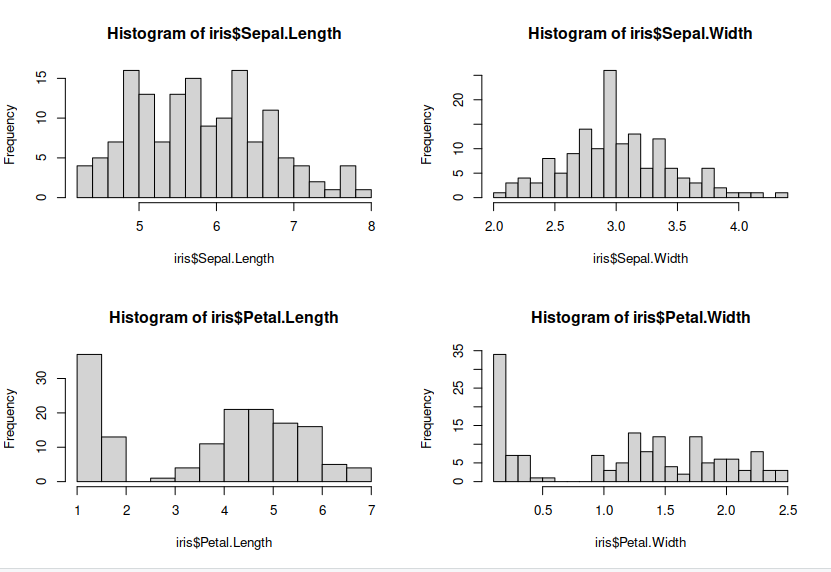
Lets make some plots looking at each of our features, so we can see the distribution of our features.
> par(mfrow = c(2, 2))
> hist(iris$Sepal.Length, breaks = 20) ## histograms for each features
> hist(iris$Sepal.Width, breaks = 20)
> hist(iris$Petal.Length, breaks = 20)
> hist(iris$Petal.Width, breaks = 20)
Principle Component Analysis (PCA)
PCA is a technique that does rotations of data in a two dimensional array to decompose the array into combinations vectors that are orthogonal and can be ordered according to the amount of information they carry. As there are as many principal components as there are variables in the data, principal components are constructed in such a manner that the first principal component accounts for the largest possible variance in the data set. Hence, when you condense your data into two dimensions, you’re essentially utilising the two principal components characterised by the highest variance.
# PCA
# Make sure you reset your variables
> data(iris)
> pc <- prcomp(iris[,-5],center = T,scale. = T) ## start PCA
> pc
> summary(pc)
Standard deviations (1, .., p=4):
[1] 1.7083611 0.9560494 0.3830886 0.1439265
Rotation (n x k) = (4 x 4):
PC1 PC2 PC3 PC4
Sepal.Length 0.5210659 -0.37741762 0.7195664 0.2612863
Sepal.Width -0.2693474 -0.92329566 -0.2443818 -0.1235096
Petal.Length 0.5804131 -0.02449161 -0.1421264 -0.8014492
Petal.Width 0.5648565 -0.06694199 -0.6342727 0.5235971
Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.7084 0.9560 0.38309 0.14393
Proportion of Variance 0.7296 0.2285 0.03669 0.00518
Cumulative Proportion 0.7296 0.9581 0.99482 1.00000
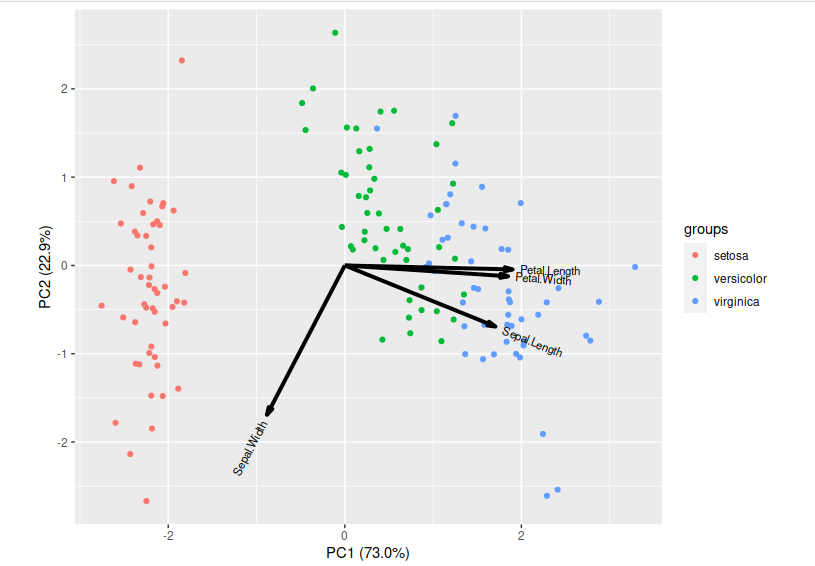
Now lets visualise our reduced features:
> library(ggbiplot)
> ggbiplot(pc,obs.scale = 1, var.scale = 1, groups = iris$Species) ##plot our pca results
t-distributed Stochastic Neighbor Embedding (t-SNE)
t-SNE is a statistical approach used to visually represent high-dimensional data by assigning each data point a position on a two- or three-dimensional map. Unlike linear techniques, t-SNE is nonlinear and is particularly effective for reducing the dimensionality of data to enable visualization in a lower-dimensional space. It accomplishes this by modeling each high-dimensional object as a point in two or three dimensions, ensuring that similar objects are positioned close together while dissimilar ones are placed farther apart with high probability.
# t-SNE embedding
> library(tsne)
> features <- subset(iris, select = -c(Species)) ### create a subset data frame without the species labels
> set.seed(0)
> tsne <- tsne(features, initial_dims = 2) ### lets reduce our features from 4 dimension to 2
> tsne <- data.frame(tsne) ## put it in data frame so its easier to use
> pdb <- cbind(tsne,iris$Species) ## add back in the labels
> summary(tsne)
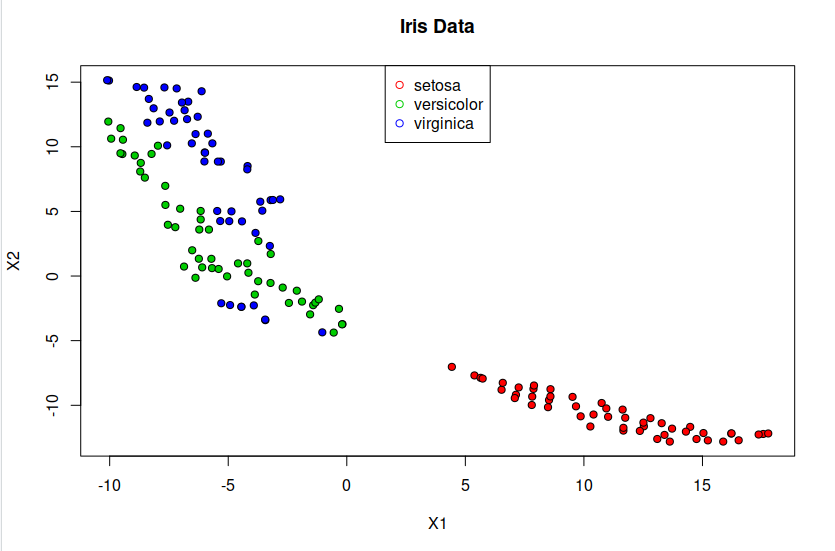
X1 X2
Min. :-16.857 Min. :-5.276300
1st Qu.:-10.994 1st Qu.:-2.199154
Median : -2.691 Median : 0.009581
Mean : 0.000 Mean : 0.000000
3rd Qu.: 12.147 3rd Qu.: 2.051889
Max. : 20.724 Max. : 5.731033
> plot(tsne, pch=21, bg=c("red","green3","blue")[unclass(iris$Species)], main="Iris Data") ## plot tsne
> legend("top",levels(iris$Species), pch = 21, col = c("red","green3","blue"))
Exercise: Parameters
Look up parameters that can be changed in PCA and t-SNE, and experiment with these. How do they change your resulting plots? Might the choice of parameters lead you to make different conclusions about your data?
Exercise: Other Algorithms
There are other algorithms that can be used for doing dimensionality reduction, for example the Higher Order Singular Value Decomposition (HOSVD) Do an internet search for some of these and examine the example data that they are used on. Are there cases where they do poorly? What level of care might you need to use before applying such methods for automation in critical scenarios? What about for interactive data exploration?
Key Points
Regression
Overview
Teaching: min
Exercises: minQuestions
Objectives
Linear regression
We now create a basic linear model for a given dataset. It would be valuable to assess the accuracy of this model. One way to achieve this is by computing the predicted y-values for each x-value in our original dataset and comparing them with the actual y-values. We can aggregate these individual discrepancies into a single comprehensive error metric by calculating the least squares. This involves squaring each difference, summing them all, dividing the sum by the total number of observations, and then taking the square root of the result. By squaring and subsequently taking the square root, we prevent negative errors from offsetting positive ones, thus providing us with an overall error metric to gauge the accuracy of our model.
Preprocess the dataset
Any easy way to calculate our intercepts is to use least squares fit.
> lsfit(iris$Petal.Length, iris$Petal.Width)$coefficients # find linear fit intercepts
Intercept X
-0.3630755 0.4157554 .4
So now we have our intercepts, lets plot our line of best fit to our data.
> plot(iris$Petal.Length, iris$Petal.Width, pch=21, bg=c("red","green3","blue")[unclass(iris$Species)], main="Edgar Anderson's Iris Data", xlab="Petal length", ylab="Petal width")
> abline(lsfit(iris$Petal.Length, iris$Petal.Width)$coefficients, col="black") ### plot the clusters with linear line.
> legend("top",levels(iris$Species), pch = 21, col = c("red","green3","blue"))
So lets now have ago at building a linear model instead using “lm”
> lm_fit <- lm(Petal.Width ~ Petal.Length, data=iris) ## create linear model
> lm_fit$coefficients
(Intercept) Petal.Length
-0.3630755 0.4157554
Again lets plot our linear model
> plot(iris$Petal.Length, iris$Petal.Width, pch=21, bg=c("red","green3","blue")[unclass(iris$Species)], main="Edgar Anderson's Iris Data", xlab="Petal length", ylab="Petal width")
> abline(lm(Petal.Width ~ Petal.Length, data=iris)$coefficients, col="black") ## plot linear model
> legend("top",levels(iris$Species), pch = 21, col = c("red","green3","blue"))
We can also look at how well our linear model fits the data by examining the p values and also have our model predict values for Petal width.
> summary(lm(Petal.Width ~ Petal.Length, data=iris))
> newdata = data.frame(Petal.Length=c(2,3,5)) ##create dataframe of features to predict
> predict(lm_fit, newdata) ## predict linear model
Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)
Residuals:
Min 1Q Median 3Q Max
-0.56515 -0.12358 -0.01898 0.13288 0.64272
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.363076 0.039762 -9.131 4.7e-16 ***
Petal.Length 0.415755 0.009582 43.387 < 2e-16 ***
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2065 on 148 degrees of freedom
Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266
F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16
Prediction Results
1 2 3
0.4684353 0.8841907 1.7157016
Try different features
Have ago at using the same code and trying with sepal instead of petal, or any combination.
Logistic Regression
We’ve now seen how we can use linear regression to make a simple model and use that to predict values, but what do we do when the relationship between the data isn’t linear?
Logarithms Introduction
Logarithms are the inverse of an exponent (raising a number by a power).
log b(a) = c b^c = aFor example:
2^5 = 32 log 2(32) = 5If you need more help on logarithms see the Khan Academy’s page
This time instead of focusing on plotting, were going to use logistic regression as a classifier. First we need to prepossess our data set by splitting it into training and test data. Then we will apply logistic regression using the binomial family using the sepal length feature.
> library(caTools)
> set.seed(1)
> split = sample.split(iris$Sepal.Length, SplitRatio = 0.75) ## create dataset split
> train = subset(iris, split==TRUE) ## train split
> test = subset(iris, split==FALSE) ## test split
> y<-train$Species; x<-train$Sepal.Length ## use sepal length as features
> glfit<-glm(y~x, family = 'binomial')
> summary(glfit)
## Call: ## glm(formula = y ~ x, family = "binomial") ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.94538 -0.50121 0.04079 0.45923 2.26238 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -25.386 5.517 -4.601 4.20e-06 *** ## x 4.675 1.017 4.596 4.31e-06 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 110.854 on 79 degrees of freedom ## Residual deviance: 56.716 on 78 degrees of freedom ## AIC: 60.716 ## ## Number of Fisher Scoring iterations: 6
So we have now created our model and we want to predict some of the samples in our test set.
> newdata<- data.frame(x=test$Sepal.Length) ## convert data into dataframe
> predicted_val<-predict(glfit, newdata, type="response") ## predict test set
> prediction<-data.frame(test$Sepal.Length, test$Species,predicted_val) ## cast prediction to dataframe
> prediction
test.Sepal.Length test.Species predicted_val 1 4.6 setosa 0.014429053 2 5.0 setosa 0.098256223 3 4.8 setosa 0.038406518 4 5.4 setosa 0.447809228 5 5.1 setosa 0.152523368 6 4.9 setosa 0.061887119 7 4.4 setosa 0.005337797 8 5.1 setosa 0.152523368 9 5.0 setosa 0.098256223 10 6.4 versicolor 0.991906259 11 6.5 versicolor 0.995084059 12 5.2 versicolor 0.229146102 13 6.1 versicolor 0.964535637 14 5.6 versicolor 0.688708107 15 5.9 versicolor 0.908836090 16 6.8 versicolor 0.998904845 17 6.7 versicolor 0.998192419 18 5.5 versicolor 0.572554250 19 5.8 versicolor 0.857868639 20 5.4 versicolor 0.447809228 21 6.0 versicolor 0.942746684 22 6.3 versicolor 0.986701696 23 5.6 versicolor 0.688708107 24 5.5 versicolor 0.572554250 25 5.7 versicolor 0.785142952 26 4.9 virginica 0.061887119 27 7.2 virginica 0.999852714 28 5.7 virginica 0.785142952 29 5.8 virginica 0.857868639 30 6.4 virginica 0.991906259 31 6.1 virginica 0.964535637 32 7.7 virginica 0.999988017 33 6.3 virginica 0.986701696 34 6.0 virginica 0.942746684 35 6.9 virginica 0.999336667 36 6.7 virginica 0.998192419 37 6.2 virginica 0.978223885
Looking at our results, the prediction val column give thew prediction confidence that said belongs to that class. typically in machine learning we use the 0.5 confidence threshold. Now lest have a look at what our chat looks like.
> qplot(prediction[,1], round(prediction[,3]), col=prediction[,2], xlab = 'Sepal Length', ylab = 'Prediction using Logistic Reg.') ## plot our predictions
trying different features
Again have ago at using different features to see what changes in the prediction.
Key Points
day 1 practical
Overview
Teaching: min
Exercises: minQuestions
Objectives
Excerise 1
There were exercises throughout the sections that we covered today. If you didn’t get chance to do them then please go back and have ago at them now. If completed, go on to exercise 2.
Excercise 2
Please use the download link to be able to access the penguin dataset which will be used for this exercise.
Task 1:
Using the penguin dataset do some k-means clustering using the features: bill_length_mm, bill_depth_mm, flipper_length_mm, body_mass_g and species as the labels. Use any combination of the features you want. Please produce a plot of your results of k-means. Do the same again but with Spectral clustering and a plot would be nice.
Task 2:
Now its time to do some dimensional reduction, so using PCA and Tsne please create a plot of your data using each method. If you want to be adventurous, try reducing them to 3 dimension and creating a 3D plot.
Task 3:
Have ago at fitting a linear and Logistic Regression models to your data. again plots would be nice.
Key Points
Non-Linear Classifiers
Overview
Teaching: min
Exercises: minQuestions
Objectives
K-Nearest Neighbour (KNN)
The k-nearest Neighbours algorithm, commonly referred to as KNN or k-NN, is a supervised learning classifier that falls under the non-parametric category. It leverages proximity to classify or predict the grouping of a specific data point. Although it can tackle both regression and classification tasks, it is predominantly employed as a classification tool. The underlying principle is based on the assumption that similar data points tend to cluster together. In classification scenarios, the algorithm assigns a class label through a majority vote mechanism. In other words, the label that appears most frequently among neighboring data points is adopted. While technically termed “plurality voting,” it is often referred to as “majority vote” in literature. The distinction lies in the requirement for a true majority (over 50%), which suits binary classification situations. In cases involving multiple classes (e.g., four categories), a conclusive decision regarding a class label can be made with a threshold vote exceeding 25%.
Before we train any non-linear machine learning models, we need to divide our data into train and test sets. To do this we use a library called caTools. Furthermore, traditionally machine learning models only accept inputs which are between zero and one. so we will also need to scale our data.
> library(caTools)
> set.seed(1)
> split = sample.split(iris$Sepal.Length, SplitRatio = 0.75)
> train = subset(iris, split==TRUE)
> test = subset(iris, split==FALSE)
> train_scaled = scale(train[-5])
> test_scaled = scale(test[-5])
> train_scaled
Sepal.Length Sepal.Width Petal.Length Petal.Width setosa virginica versicolor 5.8522124 3.0663717 3.6734513 1.1513274 0.3628319 0.3362832 0.3008850 attr(,"scaled:scale") Sepal.Length Sepal.Width Petal.Length Petal.Width setosa virginica versicolor 0.8523180 0.4524952 1.8304477 0.7617080 0.4829586 0.4745415 0.4606857
Now lets build our self KNN model, which we use a library called class.
> library(class)
> test_pred <- knn(train = train_scaled, test = test_scaled,cl = train$Species, k=2)
> test_pred
[1] setosa setosa setosa setosa setosa setosa setosa setosa setosa versicolor versicolor [12] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor [23] versicolor versicolor versicolor virginica virginica virginica virginica virginica virginica virginica virginica [34] virginica virginica virginica virginica Levels: setosa versicolor virginica
Confusion Matrix
To look at how our model performed, there are a number of ways you could look at it. The best way is to have look at the confusion matrix and luckily in R there is a built in function that does this for us. All we have to do is pass our prediction results to the table function. Furthermore, by summing the diagonal and dividing by the length of our test set we can come up with an accuracy value.
> actual <- test$Species
> cm <- table(actual,test_pred)
> cm
> accuracy <- sum(diag(cm))/length(actual)
> sprintf("Accuracy: %.f%%", accuracy*100)
"Accuracy: 92%"
test_pred
actual setosa versicolor virginica
setosa 9 0 0
versicolor 0 16 0
virginica 0 3 9
Support Vector Machines (SVM)
The Support Vector Machine (SVM) emerges as a formidable supervised algorithm, demonstrating its effectiveness particularly on smaller yet intricate datasets. While adept at handling both regression and classification tasks, SVMs notably shine in classification scenarios. Originating in the 1990s, SVMs garnered widespread recognition and endure as a favoured option for high-performance algorithms, often requiring minimal adjustments to yield robust outcomes. Described as a machine learning algorithm utilising supervised learning models, SVMs tackle intricate classification, regression, and outlier detection challenges by executing optimal data transformations. These transformations delineate boundaries between data points based on predefined classes, labels, or outputs. This article elucidates the core principles of SVMs, their functionality, variations, and offers insights through real-world illustrations.
Strengths of support vector machines:
- Effective in navigating high-dimensional spaces.
- Remain potent even when faced with a higher number of dimensions compared to samples.
- Operate efficiently on memory by utilizing a subset of training points known as support vectors in the decision-making process.
- Offer versatility through the option to specify various Kernel functions for the decision function, including the provision for custom kernels.
Drawbacks of support vector machines:
- When the number of features significantly exceeds the number of samples, guarding against over-fitting necessitates careful selection of Kernel functions and regularization terms.
- Direct probability estimates are not provided by SVMs; obtaining such estimates involves resource-intensive techniques like five-fold cross-validation (refer to Scores and probabilities).
SVM in R
So to create a SVM model, we are going to use the library called “e1071”. We are also going to use our train/test separations from above.
> library(e1071)
> Species <- train$Species
> svm_model <- svm(Species ~ ., data=train_scaled, kernel="linear") #linear/polynomial/sigmoid
Now lets have ago at predicting our test set using the SVM model. Again we are going to produce a confusion matrix and generate an accuracy score.
> pred = predict(svm_model,test_scaled)
> tab = table(Predicted=pred, Actual = test$Species)
> tab
> accuracy <- sum(diag(tab))/length(test$Species)
> sprintf("Accuracy: %.f%%", accuracy*100)
"Accuracy: 92%"
Actual
Predicted setosa versicolor virginica
setosa 9 0 0
versicolor 0 16 3
virginica 0 0 9
different non-linear classifier
Have ago at implementing a different non-linear classifier. examples of decision tree can be found at: https://www.datacamp.com/tutorial/decision-trees-R Or even Random forest: https://www.r-bloggers.com/2021/04/random-forest-in-r/
Key Points
Neural Networks
Overview
Teaching: min
Exercises: minQuestions
Objectives
Introduction
Neural networks, drawing inspiration from the workings of the human brain, represent a machine learning approach adept at discerning patterns and categorizing data, frequently leveraging images as input. This technique, rooted in the 1950s, has evolved through successive iterations, surmounting inherent constraints. Today, the pinnacle of neural network advancement is often denoted as deep learning.
Perceptrons
Perceptrons serve as the foundational units within neural networks, mirroring the functionality of individual neurons in the brain. Typically equipped with one or more inputs and a solitary output, they operate by weighting each input and aggregating these weighted values. Subsequently, the summed result undergoes evaluation by an activation function, determining whether the neuron emits a signal. While some activation functions employ a straightforward threshold step mechanism, delineating between zero and one based on input magnitude, alternative designs may utilize different functions. Nevertheless, these functions commonly yield outputs ranging from zero to one and retain a step-wise characteristic.
Coding a perceptron
The function requires three parameters: Inputs, a list of input values; Weights, a list of weight values; and Threshold, denoting the activation threshold. Initially, we perform element-wise multiplication of each input with its corresponding weight. Subsequently, the total sum of these products is computed. If this sum falls below the activation threshold, the output is zero; otherwise, it is one.
Perceptron limitations
A solitary perceptron is incapable of resolving any function that lacks linear separability, necessitating the ability to partition input and output classes with a straight line. An illustrative instance is the XOR function below:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
(Make a graph of this)
which yields zero output when all inputs are either one or zero, defying straightforward linear separation. This inadequacy, termed linear separability, was recognized in the 1960s, leading to a stagnation in neural network advancement for over a decade, often referred to as the “AI Winter.”
Multi-layer Perceptrons
A single perceptron lacks the capability to address functions that lack linear separability. To tackle such nonlinear challenges, we rely on multiple perceptrons, often organized into several layers. These layers constitute networks of artificial neurons, each capable of processing one or more inputs and producing a single output. The neurons interconnect within expansive networks, commonly comprising tens to thousands of units. Typically, these networks are structured in layers, encompassing an input layer, one or more hidden layers, and ultimately, an output layer.
Training Multi-layer perceptrons
Multi-layer perceptrons need to be trained by showing them a set of training data and measuring the error between the network’s predicted output and the true value. Training takes an iterative approach that improves the network a little each time a new training example is presented. There are a number of training algorithms available for a neural network today, but we are going to use one of the best established and well known, the backpropagation algorithm. The algorithm is called back propagation because it takes the error calculated between an output of the network and the true value and takes it back through the network to update the weights. If you want to read more about back propagation, please see this chapter from the book “Neural Networks - A Systematic Introduction”.
Multi-layer perceptrons training in R
We’re preparing to construct a multi-layer perceptron to predict species in the iris dataset. With the dataset’s four computed features representing two aspects of the plant, along with width and height, we’ll set up four input neurons. The number of hidden layers can vary and is typically determined through experimentation. Since there are three different species of plants, we’ll incorporate three output neurons.
Before delving into the construction, let’s organize our data for ingestion into the neural network:
> data(iris)
> iris$setosa <- iris$Species=="setosa"
> iris$virginica <- iris$Species == "virginica"
> iris$versicolor <- iris$Species == "versicolor"
> iris.train.idx <- sample(x = nrow(iris), size = nrow(iris)*0.5)
> iris.train <- iris[iris.train.idx,]
> iris.valid <- iris[-iris.train.idx,]
Now lets build our neural network, to which we use a library called neuralnet:
> iris.net <- neuralnet(setosa+versicolor+virginica ~
Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
data=iris.train, hidden=c(10,10), rep = 5, err.fct = "ce",
linear.output = F, lifesign = "minimal", stepmax = 1000000,
threshold = 0.001)
hidden: 10, 10 thresh: 0.001 rep: 1/5 steps: 1763 error: 0.00011 time: 0.29 secs hidden: 10, 10 thresh: 0.001 rep: 2/5 steps: 661 error: 0.00035 time: 0.1 secs hidden: 10, 10 thresh: 0.001 rep: 3/5 steps: 688 error: 0.00044 time: 0.1 secs hidden: 10, 10 thresh: 0.001 rep: 4/5 steps: 1014 error: 0.00018 time: 0.15 secs hidden: 10, 10 thresh: 0.001 rep: 5/5 steps: 1023 error: 0.00023 time: 0.15 secs
Now lets take a look at our trained neural network:
> plot(iris.net, rep="best")
Prediction using a multi-layer perceptron
Confusion Matrix
To look at how our model performed, there are a number of ways you could look at it. The best way is to have look at the confusion matrix and luckily in R there is a built in function that does this for us. All we have to do is pass our prediction results to the table function. Furthermore, by summing the diagonal and dividing by the length of our test set we can come up with an accuracy value.
> iris.prediction <- compute(iris.net, iris.valid[-5:-8])
> idx <- apply(iris.prediction$net.result, 1, which.max)
> predicted <- c('setosa', 'versicolor', 'virginica')[idx]
> cm <- table(predicted, iris.valid$Species)
> accuracy <- sum(diag(cm))/length(iris.valid$Species)
> sprintf("Accuracy: %.f%%", accuracy*100)
predicted setosa versicolor virginica setosa 25 0 0 versicolor 0 23 2 virginica 0 2 23 [1] Accuracy: 95%
Changing the different characteristics of the neural network
There are a number of characteristics you can change in your model, that may increase or decrease the performance of your model. have ago at adjusting the number of steps, linear output (“T” or “F”) and number of hidden layers.
Cloud APIs
Google, Microsoft, Amazon, and many others now have Cloud based Application Programming Interfaces (APIs) where you can upload an image and have them return you the result. Most of these services rely on a large pre-trained (and often proprietary) neural network.
Exercise: Try cloud image classification
Take a photo with your phone camera or find an image online of a common daily scene. Upload it Google’s Vision AI example at https://cloud.google.com/vision/ How many objects has it correctly classified? How many did it incorrectly classify? Try the same image with Microsoft’s Computer Vision API at https://azure.microsoft.com/en-gb/services/cognitive-services/computer-vision/ Does it do any better/worse than Google?
Existing API’s of machine learning models
A vast collection of deep learning machine models can be found on the platform known as Hugging Face. Serving as an AI community hub, it offers a diverse array of pre-trained, cutting-edge machine learning models accessible to all users.
Exercise: Existing API’s of machine learning models
go to https://huggingface.co/ and have ago at some of the different models, alot of them have inference API so you can have ago on the website.
Key Points
Ethics and Implications of Machine Learning
Overview
Teaching: min
Exercises: minQuestions
Objectives
Ethics and Machine Learning
There are increasing worries about the ethics of using machine learning. In recent year’s we’ve seen a number of worrying problems from machine learning entering all kinds of aspects of daily life and the economy:
- The first death from an autonomous car which failed to brake for a pedestrian.[1]
- Highly targetted advertising based around social media and internet usage. [2]
- The outcomes of elections and referendums being influenced by highly targetted social media posts . This is compunded by the data being obtained without the users’s consent. [3]
- The mass deploymeny of facial recognition technologies. [4]
- The possible first use of autonomous military robots making a decision to kill in battle. [5]
Problems with bias
Machine learning systems are often presented as more impartial and consistent ways to make decisions. For example sentencing criminals or deciding if somebody should be granted bail. There have been a number of examples recently where machine learning systems have been shown to be biased because the data they were trained on was already biased. This can occur due to the training data being unrepresentative and under representing certain groups. For example if you were trying to automatically screen job candidates and used a sample of people the same company had previously decided to employ then any biases in their past employment processes would be reflected in the machine learning.
Problems with explaining decisions
Many machine learning systems (e.g. neural networks) can’t really explain their decisions. Although the input and output are known trying to explain why the training caused the network to behave in a certain way can be very difficult. If a decision is questioned by a human its difficult to provide any rationale as to how a decision was arrived at.
Problems with accuracy
No machine learning system is ever 100% accurate. Getting into the high 90s is usually considered good. But when we’re evaluating millions of data items this can translate into 100s of thousands of mis-identifications. If the implications of these incorrect decisions are serious then it will cause major problems. For instance if it results in somebody being imprisoned or even investigated for a crime or maybe just being denied insurance or a credit card.
Energy Usage
Many machine learning systems (especially deep learning) need vast amounts of computational power which in turn can consume vast amounts of energy. Depending on the source of that energy this might account for significant amounts of fossil fuels being burned. It is not uncommon for a modern GPU accelerated computer to use several kilowatts of power, running this for one hour could easily use as much energy a typical home would use in an entire day. This can be particularly bad when models are constantly being retrained or when “parameter sweeps” are done to find the best set of parameters to train with.
Ethics of machine learning in research
Not all research using machine learning will have major ethical implications. Many research projects don’t directly affect the lives of other people, but this isn’t always the case.
Some questions you might want to ask yourself (and which an ethics committee might also ask you):
- Will anything your machine learning system does make a decision that somehow affects a person’s life?
- Will anything your machine learning system does make a decision that somehow affects an animial’s life?
- Will you be using any people to create your training data? Will they have to look at any disturbing or traumatic material during the training process?
- Are there any inherent biases in the dataset(s) you’re using for training?
- How much energy will this computation use? Are there more efficient ways to get the same answer?
Exercise: Ethical implications of your own research
Split into pairs or groups of three. Think of a use case for machine learning in your research areas. What ethical implications (if any) might there be from using machine learning in your research? Write down your group’s answers in the etherpad.
Key Points
Find out more
Overview
Teaching: min
Exercises: minQuestions
Objectives
Other algorithms
There are many other machine learning algorithms that might be suitable for helping to answer your research questions.
The Scikit Learn webpage has a good overview of all the features available in the library.
Ensemble Learning
Ensemble Learning is a technique which combines multiple machine learning algorithms together to improve results. A popular ensemble technique is Random Forest which creates a “forest” of decision trees and then tries to prune it down to the most effective ones. Its a flexible algorithm that can work both as a regression and a classification system. See the article Random Forest Simple Explanation for more information.
Genetic Algorithms
Genetic algorithms are a technique which tries to mimic biological evolution. They will learn to solve a problem through a gradual process of simulated evolution. Each generation is mutated slightly and then evaluated with a fitness function, the fittest “genes” will then be selected for the next generation. Sometimes this is combined with neural networks to change the network’s size structure.
This video shows a genetic algorithm evolving neural networks to play a video game.
Useful Resources
-
Machine Learning for Everyone - A useful overview of many different machine learning techniques, all introduced in an easy to follow way.
-
Google machine learning crash course - A quick course from Google on how to use some of their machine learning products.
-
Facebook Field Guide to Machine Learning - A good introduction to machine learning concepts from Facebook.
-
Amazon Machine Learning guide - An introduction to the key concepts in machine learning from Amazon.
-
Azure AI - Microsoft’s Cloud based AI platform.
Key Points
day 2 practical
Overview
Teaching: min
Exercises: minQuestions
Objectives
Excerise 1
There were exercises throughout the sections that we covered today. If you didn’t get chance to do them then please go back and have ago at them now. If completed, go on to exercise 2.
Excercise 2
Please use the download link to be able to access the penguin dataset which will be used for this exercise.
Task 1:
Using the penguin dataset create a KNN and SVM model using the features: bill_length_mm, bill_depth_mm, flipper_length_mm, body_mass_g and species as the labels. see if you can get your model to generate some predictions. how do they preform?
Task 2:
Now it time to create yourself a deep learning neural network to generate some predictions. again how does it perform? Have ago at altering the number of layers and see if you get a performance increase.
Task 3:
Have a think of what you believe are the ethical implications of machine learning. what could be the biggest benefit’s and what are the dangers.
Key Points